Triples Pitagóricos

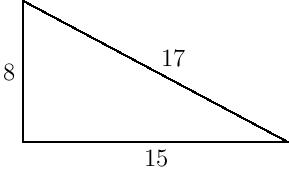
Un triple pitagórico tiene tres enteros positivos a, b y c, tales que a² + b² = c² . En otras palabras, un triple pitagórico representa las longitudes de los lados de un triángulo rectángulo en el que los tres lados tienen longitudes enteras. Este triple se suele escribir (a, b, c).

Un triple pitagórico primitivo es aquel en el que a, b y c son coprimos, es decir, que el máximo común divisor de a, b y c es 1. La siguiente es una lista de triples pitagóricos primitivos con valores inferiores a 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).

Teorema de Pitágoras recíproco

Dado un triángulo rectángulo con lados a, b, c y altitud d (una recta del ángulo recto y perpendicular a la hipotenusa c). El teorema de Pitágoras tiene, a² + b² = c² mientras que el teorema pitagórico recíproco o el teorema de Pitágoras al revés relaciona las dos catetos a, b con la altitud d, ¹/_a² + ¹/_b² = ¹/_d²

La ecuación se puede transformar en, ¹/_(x*z)² + ¹/_(y*z)² = ¹/_(x*y)² donde x² + y² = z² para cualquier real no nulo x, y, z.

Si los a, b, d han de ser enteros, la solución más pequeña a > b > d es entonces ¹/₂₀² + ¹/₁₅² = ¹/₁₂² utilizando el triple pitagórico más pequeño 3, 4, 5. El teorema de Pitágoras recíproco es un caso especial de la ecuación óptica ¹/_p + ¹/_q = ¹/_r